Protože diferenciální rovnice na počítači byly jedním z mých oblíbených jídel, eh, vlastně předmětů, rozhodla jsem se s nimi taky zasvinit svůj web. Nebudu tady přepisovat látku celého semestru. Řešení obyčejných diferenciálních rovnic známe všichni už ze školky (strýčkové Runge a Kutta, různí střelci a jiní lovci průběhů diferenciálek..), proto se vrhneme na modelový příklad řešení jedné parciálky. Jedná se o zkouškový příklad, který jsem dostala.

I. Zadání
Navrhněte diferenční schéma pro rovnici utt=a²uxx na třech bodech v n-té časové vrstvě a jednom bodu na (n+1) a (n-1) časové vrstvě. K navrženému schématu navíc stanovte řád přesnosti, obor stability, modifikovanou rovnici (toto vše v programu Maple) a na závěr schéma implementujte v programu Matlab.

II. Návrh schématu
Zadání bychom tedy měli. K úloze jsem dostala pár chytrých papírů, které velmi pomohly pri určování stability. Nejdříve ale návrh. Pro návrh schématu jsem použila Maple (zde je zdroják), ale upřímně - nebyl vlastně ani potřeba. Každý ví, že na třech bodech se toho moc kouzlit nedá, pokud chceme druhou derivaci. Takže pro ty, kdo sice ví, jak náhrada vypadá ale už si nepamatují, jak se k ní dojde: Diferenční náhrada za druhou prostorovou derivaci bude mít obecně tvar

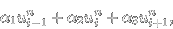
kde i značí prostorovou vrstvu a n časovou vrstvu. Podobně druhá derivace podle času bude mít tvar

.

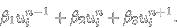Soustavu pro neznámé koeficienty α a β, kterou získáme rozvinutím u(t,x) do Taylorovy řady, vyřešíme a výsledkem je hledané diferenční schéma:

.

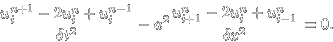III. Řád přesnosti
Řád přesnosti získáme rozvinutím u do Taylorovy řady a jeho následným dosazením do výše uvedeného diferenčního schématu. Nejnižší mocniny δt a δx ve výsledku udávají řád přesnosti v t resp. v x. Mnou navržené schéma je řádu O(δt²,δx²). (Opět maplovský zdroják, kde je postup pěkně vidět.)

IV. Stabilita
Pro zjištění oboru stability je nutné vyjádřit nejprve zesilující faktor g, který získáme z von Neumannovy analýzy schématu. Protože se jedná o vícekrokové schéma v čase, budeme vyšetřovat kořeny charakteristického polynomu. Pouzijeme známou fintu s dosazením:

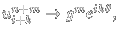
kde θ = δxξ. Po dosazení získáme výraz

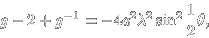
kde λ = δt/δx. ( Zde je opět .mws soubor, použila jsem z něj vlastně jen začátek, tedy dosazení, další úpravy pokračovaly na papíře. ;) ) Výraz hravě upravíme

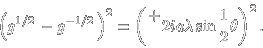
a už jsme skoro doma. Odmocníme a zpřeházíme takto:

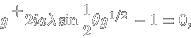
což je kvadratická rovnice jejíž kořeny jsou

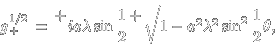
tedy můžeme psát

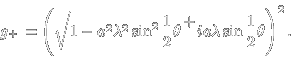
Zesilující faktor g musí být menší nebo roven 1, aby bylo schéma stabilní. Je vidět, že |g| je omezeno jedničkou pouze pokud aλ bude menší nebo rovno jedné.

V. Modifikovaná rovnice
Při určování modifikované rovnice se postupuje nejprve stejně jako při určování řádu přesnosti. Všechny časové derivace řádu vyššího než dva se dále nahrazují prostorovými a smíšenými derivacemi. Členy s mocninou δx a δt větší než čtyři lze též zanedbat. Modifikovaná rovnice pro navržené schéma má tvar

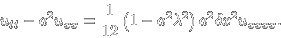
Dalším zkoumáním modifikované rovnice bychom mohli zjistit, že ji lze von Neumannovou analýzou rozložit do dvou různých vln, lišících se od sebe pouze znamínkem, tedy představují dva různé směry pohybu vlny.(Zdroják ke stažení.) Pozn.: U schémat popisujících druhou a vyšší derivace se ale rozbor modifikované rovnice většinou nedělá.

VI. Implementace
Pro implementaci byl použit dle rozkazu programový balík Matlab. Pro inicializaci jsem použila schéma, ve kterém je daná počáteční vlna v čase t=0 a první časová vrstva se z ní spočte pomocí prvních členů Taylorova rozvoje

Je vidět, že k dosazení je třeba nejdřív vyjádřit diferenční náhradu za ut a utt. Protože utt = a²uxx, lze za utt dosadit z výše uvedeného diferenčního schématu

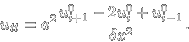
Za ut jsem použila jednoduchou diferenční náhradu

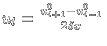
Tím jsem získala nultou (počáteční) a první časovou vrstvu, další vrstvy se již počítají podle výše odvozeného schématu. Naprogramovaná implementace je ke stažení zde , spouští se souborem pde.m. Naimplementovala jsem ještě podobné schéma na sedmi bodech - n-tá časová vrstva byla bohatší o dva body. Postup odvození schématu, řádu přesnosti, stability atd. je stejný jako v pětibodovém schématu, které jsem právě popsala. Matlabová implementace sedmibodového schématu je zde . Koeficient a je nastaven na optimální hodnotu, kdy je schéma nejvíce stabilní.